The Aurora Blue packaging box has become a trendy logo, and the Dewu App has become the spiritual belonging of young hipsters. The special packaging materials have formed a strong mind among consumers, and Aurora Blue is equal to Dewu.
However, since the early box size data was designed by manual experience, there was a problem that the size of the box and the size of the product did not match well, which generally caused the following effects:
- Unreasonable carton size leads to the use of larger cartons for some products, resulting in a waste of carton procurement costs.
- Larger cartons will increase shipping costs.
- Excessive space between the product and the carton may cause damage to the product during transportation.
Considering the rhythm of carton bidding and the time left for proofing and trial installation and trial delivery in the warehouse, it is necessary to complete the modeling and calculation at a relatively fast speed.
In this matter, the business side cannot give some particularly clear guidelines. For example, the specific comprehensive target to be calculated includes the transportation cost, which includes the carrier’s allocation algorithm rules and their freight template. It is basically impossible to directly incorporate factors into box modeling. For example, the number of boxes affects the cost of procurement bidding negotiations and the labor efficiency in the warehouse. It is difficult to quantify here, and it is impossible to directly define the value of the number of boxes. Judgment criteria. Therefore, we must first analyze the status quo with the business side’s products to define the goals, quantify all the problems, and simplify the problems at the same time.
2.1 Problem Analysis
sku data: The master data of the sku shipped in the past year and its corresponding sales volume, and the exclusion rules (only consider products packaged in cartons, and exclude products packed in boxes of the opposite sex) and outliers (such as abnormal sku size).
Constraints on carton size parameters: Considering the size of the face sheet (the definition of the lower limit of the size of the carton) and the rationality of packing convenience for the personnel in the warehouse (the definition of the upper limit of the size of the carton), we have determined the upper and lower limits of the carton, forming a space for millions of combinations.
Constraints on the number of boxes: excluding special-shaped boxes, it is necessary to comprehensively consider the packing rate, procurement cost and efficiency in the warehouse. Generally speaking, the number of boxes in a single warehouse should not exceed 15.
Coverage constraints: On the premise that the SKUs packed in the outer packaging of the carton have been screened, some special-shaped and large items cannot be covered by the box group, and the coverage rate of delivery orders is required to be >=99%.
Based on the above analysis of the problem, it can be seen that if there is a set of solution K box types to calculate the packing rate, the complexity of this problem is not bad. However, if the calculation is performed head-on, it is necessary to traverse the box combination for the eligible SKUs, which basically cannot calculate the result within the valid time.
2.2 Problem simplification
2.2.1 Constraints on the number of boxes
Excluding special-shaped boxes, based on the actual situation in the warehouse of Dewu, it is estimated that the number of newly designed boxes is 8~15. It is necessary to comprehensively consider the packing rate, procurement cost and efficiency in the warehouse. The box rate will increase, the procurement cost will also increase, and the efficiency in the warehouse will decrease. Since it cannot be quantified here, such as giving a specific comprehensive index, it is decided to give multiple versions here for the business side to choose, rather than as a constraint or goal of modeling, which is equivalent to directly simplifying the M groups of box types M * fixes the complexity of a box type. In actual development, only one calculation is required to be performed with M containers at the same time.
2.2.2 Coverage Constraints
The coverage constraint is an inequality constraint, and the current problem, the distribution of the uncoverable sku part is very obvious, and one or more values concentrated in the length, width, high, and high exceed the limit of the convenience of manipulation in the warehouse. Therefore, the box type is used here. Limits and areas that are not covered by acceptance are determined before modeling.
2.2.3 Objective function definition
For the purchase cost, it goes without saying that it must be related to the paper usage of the carton. The smaller the paper used for the carton (the smaller the unfolded area of the carton), the lower the cost;
For the transportation cost, basically 3pl is calculated by the method of MAX (throw weight, actual weight), then this is also positive with the optimization direction of the unfolded area of the carton;
If each 3pl freight template is added to the modeling, and the algorithm design assigned by the carrier also needs to be considered, the problem will be too complicated and the amount of calculation will be very large. Now obviously, we only need to optimize the average paper area of a single order. If the optimized carton packaging of an order does not touch the variation range of the freight template, the freight will remain unchanged. If it does, the freight cost will inevitably be reduced.
To sum up, finally consider usingPacking rateThis indirect indicator is used as the target. The packing rate refers to the test (the total volume of the data set sku / the total volume of the data set shipped boxes). This is also an indicator that the product and business parties are familiar with and have been paying attention to.
2.2.4 Problem modeling
After the above simplification, the objective function is defined as the packing rate, and the delivery order coverage and the constraint value of the number of boxes are placed outside the modeling problem.
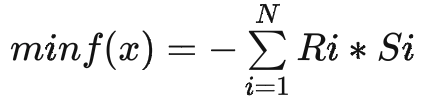
Among them, S_i represents the sales volume of Sku_i, and R_i represents the recommended box type result packing rate of Sku_i
The recommended box type should meet the internal clearance greater than the minimum requirement, select the smallest box type in the box type group, namely
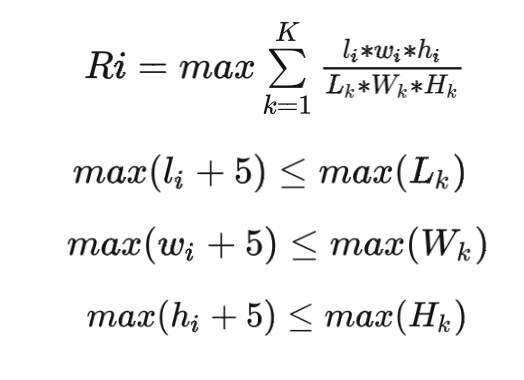
The size of the box should be at least enough for the waybill to be attached, and it should not be too large to affect the packing efficiency of the personnel in the warehouse
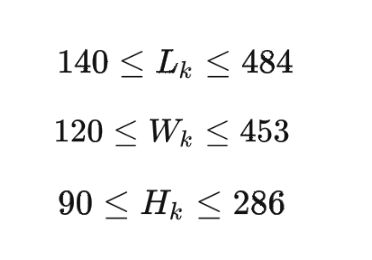
At the same time, we sort and clean the sku by length>width>height, and define the carton length>width>height
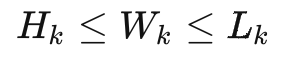
Finally, we require that the length, width and height of the box are integers, that is
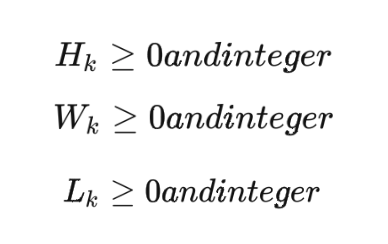
3.1 Overview of general solution methods
For this optimization problem, it usually mainly includes exact solution algorithm and heuristic algorithm:
The exact method is mainly to use the simplex method (linear programming) or some iterative methods (nonlinear programming) combined with the branch and bound method to find the integer solution we want. If the exact method is a linear programming problem, the global optimal solution can be found in the vertices of the feasible region through the simplex method, and the nonlinear programming can also find a near-optimal solution through the differential calculus method or finite iterations, because it is not polynomial time. Therefore, it is often not feasible on large-scale instances.
Heuristic algorithms such as Genetic Algorithms, Ant Colony Algorithms, Evolutionary Algorithms, and Intelligent Algorithms address common problems. Think of it as a black box for almost any problem. Heuristic algorithm, to put it bluntly, is a directional exhaustive method. In the case of limited computing resources, it is necessary to select a reasonable neighborhood structure or operation mechanism according to the problem scenario and model characteristics, between the global search ability and local search ability. Make tradeoffs. Heuristic algorithms usually require a given initial solution; in addition, algorithms are not guaranteed to converge in polynomial time, but can often control the number of algorithm iterations.

3.2 Exact solution method
For a linear programming problem, the set of feasible solutions is a convex set or an unbounded domain, and the basic feasible solution corresponds to the vertex of the convex set, and the optimal solution is obtained by the properties of the convex set. The sorting method can obtain the optimal solution, but when there are too many vertices, the simplex method needs to be used to find the optimal solution of the linear programming.
If the objective function or constraints contain nonlinear functions, for example, the current problem has nonlinear factors in the packing rate of the objective function, this programming problem is a nonlinear programming problem. Generally speaking, solving nonlinear programming problems is much more difficult than solving programming problems. It is not like the simplex method for solving linear programming. There is no general algorithm for nonlinear programming. Each method has its own specific scope of application.
Because the required output result is an integer, it needs to be solved by the branch and bound method.
The core idea of branch and bound method is branching and pruning. When the condition that the solution must be an integer is not considered, the simplex method can be used to find the optimal solution, but this solution is often not all integers, so the method of pruning is used to narrow the range little by little until the solution is an integer solution. .
As can be seen from the figure, in the initialization phase, the global upper and lower bounds of the given output are required. If there are some heuristic methods to obtain slightly better upper and lower bounds as the initial solution, it would be the best. If not, it can be set to positive and negative infinity first.
Then enter the main loop, and obtain the upper bound of the sub-problem by solving the continuous relaxation problem (linear programming) of the integer programming; the decomposition problem can help to split the integer programming problem, and can also help us get the lower bound.

3.3 Metaheuristics
Such algorithms represented by genetic algorithms are suitable for the following scenarios:
- Neural network hyperparameter optimization
- Some Combinatorial Optimization Problems with Fixed Structure and Properties
- Black-box optimization problems for which some mechanism models are difficult to establish
- multi-objective optimization problem
3.3.1 Genetic Algorithm
basic concept
- Genes: Elements of Feasible Solutions
- Chromosomes: A chromosome is a feasible solution
- Crossover: Multiple chromosomes are cut and spliced into new chromosomes
- Mutation: the modification of part of the gene of the chromosome
- Duplication: Complete genetic duplication of the previous chromosome
Implementation process
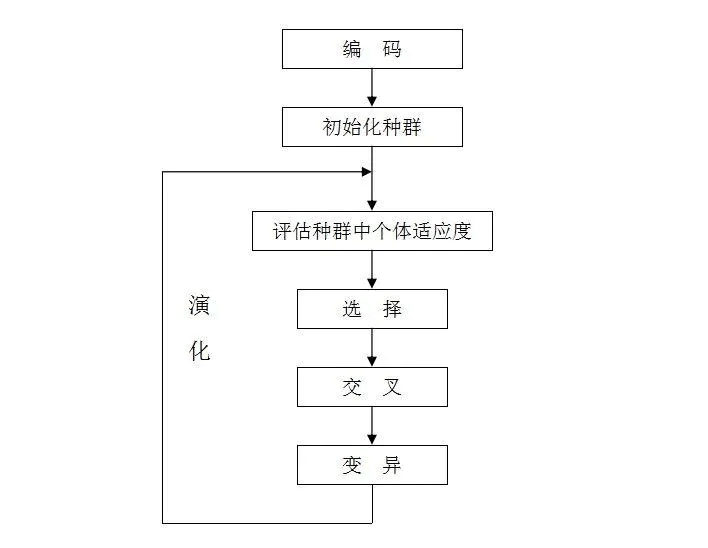
- In the initial stage of the algorithm, it randomly generates a set of feasible solutions, that is, the first generation of chromosomes.
- Then the fitness function is used to calculate the fitness of each chromosome, and the probability of each chromosome being selected in the next evolution is calculated according to the fitness.
- Through “crossover”, NM chromosomes are generated.
- Then perform “mutation” operation on the NM chromosomes generated after crossover.
- Then use the “replication” method to generate M chromosomes;
- Repeat 2~5.
4.1 Data Analysis
First of all, let’s take a rough look at the main data of the length, width and height of the sku that has been shipped in the past year and its sales distribution. This is the basis for our design of the box. At the same time, considering the efficiency of the actual operation in the warehouse and the cost of procurement, the number of boxes should not be too many, otherwise it will increase the difficulty of packing personnel in the warehouse to pick up the boxes, and the procurement cost will also increase accordingly.
In this step, considering the accuracy and the current box type A/B first, the addition of 8 to 15 types to the modeling parameters also increases the computational complexity, so it is decided to fix the value of the number of boxes, first assuming fixed N types of boxes, each with three numbers in length, width and height, that is, output 3 * N parameters.
Next, we define the length>width>height of the product sku and box type. First, the data in the past year is sorted by length, width and height, and outliers are cleaned. For example, if 12 types of boxes are fixed, we will sku and box type. Clustering into 12 groups using k-means in the length, width and height dimensions.
To do this cluster analysis, on the one hand, according to the actual situation, for example, define the lower limit of the box shape in combination with the size of the single surface, and then define the upper limit of the box shape in combination with the lower limit of the box coverage rate;
On the other hand, the maximum value of each cluster can be used as the initial value of the box (actually need to add 5mm as the gap).
4.2 Constraints and Objectives
In terms of business constraints, it is only necessary to put the goods into the boxes, leaving gaps, and since the type and quantity of the boxes are determined, it is also necessary to determine the length > width > height of each group of boxes, that is
constraint_ueq = (
# 单个箱子长>宽>高
lambda x: x[1] - x[0],
lambda x: x[2] - x[1],
lambda x: x[4] - x[3],
lambda x: x[5] - x[4],
...
)
The target is the max packing rate, which is
def cal_avg_r_cached(p):
'''The objective function. input routine, return total distance.
cal_total_distance(np.arange(num_points))
'''
total_r = 0
for row in npd:
r = [-1] * box_num
for i in range(box_num):
if (row[0] <= p[3 * i]) and (row[1] <= p[3 * i + 1]) and (row[2] <= p[3 * i + 2]):
r[i] = row[4] / (p[3 * i] * p[3 * i + 1] * p[3 * i + 2])
total_r += max(r) * row[3]
print(total_r)
return -total_r / sum_cnt
4.3 Conclusion
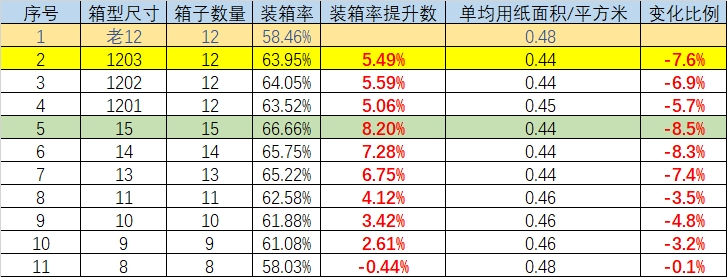
In the end, several versions were run in parallel, the packing rate was improved, and the paper area per sheet was significantly reduced;
The 1203 scheme finally selected as the output of the engineering side, the packing rate increased by 5.49%, the average paper area per unit was saved by 7.6%, and the average unit freight was reduced by 0.06 yuan.
When I wrote this article and checked relevant information, I found quite a brain hole. I used several colored triangles to assemble an image.
Here I tried to draw NONO with 60 triangles.
The effect is roughly as follows:
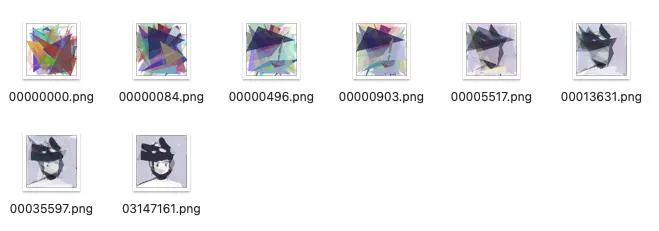
In the optimization algorithm, the general process of genetic algorithm is introduced, so what is the difference between drawing this NONO and box design?
In the box design, the box size needs to be calculated based on the packing rate index. Therefore, when defining the fitness function, you only need to take the index of Maximize packing rate. At this point, you only need to define the objective function as different The similarity between the transparent triangle assembly result of the color size and the target image is sufficient.
5.1 Fitness function
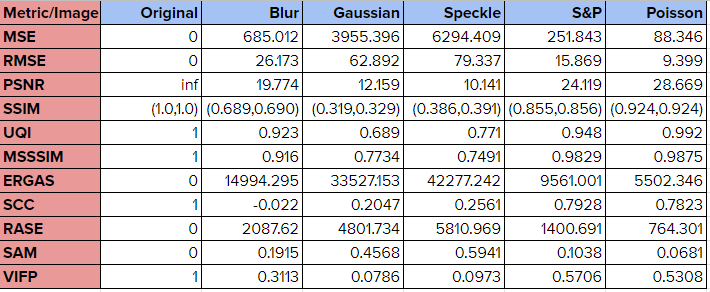
First of all, we need to find a method that can quantify the difference or similarity between the graph composed of transparent triangles and the target NONO graph. So how to define similarity? The similarity of the image is the similarity of the value vector in a certain color space (such as RGB, HSV). The minimum difference value of each point is closer to the desired target pattern. Common evaluation functions such as MSE, RMSE, PSNR, ERGAS, SAM, etc.
The following figure shows the similarity results corresponding to various similarity evaluation methods for some image noise methods. The “Original” column shows the score of the original image compared to itself.
Here ERGAS is chosen as the basis for our fitness function.
5.2 Selection
Here, the roulette method is not necessarily used to make the selection. The solution with the highest fitness function is selected with a 95% probability, and the solution is randomly selected from other solutions with a 5% probability.
if random.random() < 0.95:
'''选择基因的来源父母,95%几率从最优的祖先中随机'''
poly_a = random.choice(polygons[:1])
poly_b = random.choice(polygons[1:5])
else:
'''选择基因的来源父母,5%从所有的祖先中随机'''
poly_a = random.choice(polygons)
poly_b = random.choice(polygons)
5.3 Crossover and mutation
Random numbers are also used here, with a high probability of randomly inheriting and assigning genes from the parent class, and a small probability of modifying the gene value. The coordinate crossover mutation is roughly as follows, and the color crossover mutation is the same.
temp = random.random()
if temp < 1 / polygon_num:
'''设定一定几率坐标变异'''
rnd_temp_coord = poly_a.coord_list[i][:]
rnd_temp_coord[random.randint(0, vertices - 1)] = random.randint(0, img_width), random.randint(0, img_height)
temp_coords.append(rnd_temp_coord)
elif temp < 0.5:
'''随机继承父母中的一个基因'''
temp_coords.append(poly_b.coord_list[i])
else:
temp_coords.append(poly_a.coord_list[i])
temp = random.random()
*arts /soy sauce
Pay attention to Dewu Technology, and update technical dry goods at 18:30 every Monday, Wednesday, and Friday night
If you think the article is helpful to you, please comment, forward and like~
#Dewu #Aurora #Blue #Carton #Size #Design #Practice #Personal #Space #Dewu #Technology #News Fast Delivery